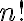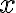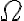Опыт преподавания теории вероятностей в математической школе
Тулякова Татьяна Виталиевна,
учитель математики высшей категории школы №598
Относительно недавно в учебную программу средней школы по математике был ввден новый раздел "Начальные главы теории вероятностей и математической статистики", который является по сути элементом высше математики. Ввиду того, что ЕГЭ по математике предполагает умение решать задачи по данной теме, то находим проблему адаптирования теоретического, практического и контрольных материалов к школьному уровню знаний и навыков восприятия актуальной. В данной статье мы хотели бы предложить варианты контрольных материалов в тестовой форме, которые могли бы помочь учителю оценивать степень понимания материала учеником после прохождения каждой темы и осуществлять регулярный контроль над восприятием нового материала. Такого рода тесты, с вопросами ориентированными именно на понимание учеником новой темы, а не на решение по аналогии с образцом данным учителем или отработку приобретенных на уроке навыков, можно и стоит проводить на каждом уроке. Особенно стоит проводить на уроках посвещенных теории вероятностей, так как в данном разделе даже на начальном уровне от ученика требуется творчекое использование материала, в силу невозможности заалгоритмизировать решение задач по указанной теме, что требует глубокого понимания материала.
Предлагаем следующие примеры тестов (физико-математический класс):
Комбинаторика
Вопрос №1
Как определяется число размещений из n элементов по k или, иначе, число всевозможных различных упорядоченных выборок объема k из данных n элементов или, иначе, число всевозможных способов выбрать k элементов из данных n элементов с учетом порядка?
Вопрос №3
Как определяется число сочетаний из n элементов по k или, иначе, число всевозможный различных неупорядоченных выборок объема k из данных n элементов или, иначе, число всевозможных способов выбрать k элементов из данных n элементов без учета порядка?
Числа размещений, сочетаний и перестановок связаны следующим соотношением
Число трёхзначных чисел, составленное из цифр 8, 7, 6, 2, 1, при условии, что все цифры в записи числа различны, равно
Пусть 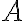 - случайное событие, тогда
- случайное событие, тогда
Из колоды в 36 карт наудачу извлечена одна карта. Случайное событие 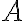 состоит в том, что вынутая карта оказалась черной масти, случайное событие
состоит в том, что вынутая карта оказалась черной масти, случайное событие 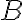 состоит в том, что вынутая карта оказалась тузом. В чем состоит случайное событие
состоит в том, что вынутая карта оказалась тузом. В чем состоит случайное событие  ?
?
Пусть 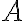 и
и 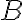 - произвольные случайные события. Выберете из нижеприведенных пар случайных событий пары, являющиеся несовместными.
- произвольные случайные события. Выберете из нижеприведенных пар случайных событий пары, являющиеся несовместными.
Случайное событие B является частным случаем случайного события A (т.е. множество элементарных исходов благоприятствующих событию B является подмножеством множества элементарных исходов благоприятствующих событию A). Чему равна сумма случайных событий A и B?
Брошены 4 игральные кости. Какова вероятность того, что на всех выпадет одинаковое число очков?
В праздничной лотерее участвуют 500 билетов , среди которых 350
выигрышных. Вероятность того, что купленный билет окажется не
выигрышным, равна
Вопрос №5
Из набора карточек с буквами К, О, Р, О, В, А наугад выбираются 3 карточки, из которых составляется слово. Какова вероятность того, что получилось слово РОВ?
Вопрос №6
3 белых и 7 чёрных шаров находятся в урне, случайным образом вынимают 3 шара. Вероятность того, что среди них два чёрных и один белый равна
Вопрос №7
Студент успел подготовить 32 вопроса из 40 экзаменационных. Вероятность получить на экзамене вопрос, который он не подготовил, равна
Вопрос №8
Экзамен по математике состоит из 25 билетов, в 9 из них встречается вопрос о свойствах логарифмов. Вероятность того, что в случайно выбранном билете достанется вопрос о свойствах логарифмов, равна
Вопрос №9
Вероятность невозможного события равна...
Вопрос №10
Пучть 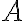 - случайное событие, тогда
- случайное событие, тогда
Если случайное событие 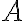 влечет случайное событие
влечет случайное событие 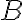 , то...
, то...
Если последовательность случайных величин  сходится к случайной величине
сходится к случайной величине 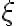 по вероятности, то она сходится к
по вероятности, то она сходится к 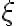 и ...
и ...
Исходным условием для расчета значения θкр правой границы двухсторонней критической области при уровне значимости α и нормальном распределении статистики критерия θn является
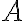 и
и 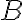 называется , что в результате случайного экперимента произойдет событие
называется , что в результате случайного экперимента произойдет событие 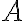 событие
событие 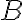 .
.
Пусть 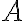 - произвольное случайное событие,
- произвольное случайное событие,  - полная группа попарно несовместных случайных событий. Формулой Байеса называется...
- полная группа попарно несовместных случайных событий. Формулой Байеса называется...
Полной группой случайных событий называется набор случайных событий  , которые удовлетворяют следующим условиям:
, которые удовлетворяют следующим условиям:
Производится следующий случайный эксперимент. Подбрасывается игральный кубик, а затем подбрасывается монета 1 раз, если на кубике выпало нечетное число очков, и 2 раза, если на кубике выпало четное число очков. Найдите вероятность того, что в результате данного эксперимента "Орел" выпадет по крайней мере один раз.
В урну, содержащую 2 шара, опущен белый шар, после чего наудачу извлечен 1 шар. Найти вероятность того, что извлеченный шар окажется белым, если равновозможны все предположения о первоначальном составе шаров по цвету.
ыберите из приведенных ниже наборов случайных событий те, которые могут быть рассмотрены как системы гипотез при использовании формул полной вероятности и Байеса.
Пусть 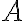 - произвольное случайное событие,
- произвольное случайное событие,  - полная группа попарно несовместных случайных событий. Формулой полной вероятности называется...
- полная группа попарно несовместных случайных событий. Формулой полной вероятности называется...