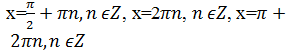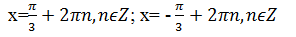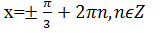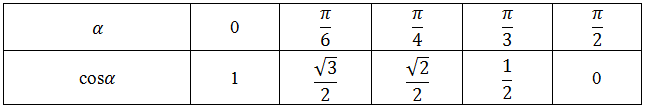Активные методы обучения на уроках математики

Елезенцева Ольга Васильевна, ГБОУ СОШ №585 г. Санкт-Петербург, учитель

«Страшная это опасность – безделье за партой; безделье шесть часов ежедневно, безделье месяцы и годы. Это развращает, морально калечит человека…».   Сухомлинский В.А.

Современный урок – это не только набор технических средств обучение, но и умение учащихся работать с текстом, записывать лекцию, вдумчивое чтение учебника. Задача учителя при такой работе добиться, чтобы ученики не просто просматривали материал, а строку за строкой прочитывали учебник, делая пометки, задавая вопросы, записывая свои мысли. Такая работа потребует от учителя немало сил, времени, самообразования.

Традиционная школа знакомила учеников с уже готовыми продуктами знаний, не показывая процессы с помощью, которых они были получены. Учащиеся привыкли работать в режиме слушания, поэтому им необходимо показать приёмы работы с текстом. Ученика надо научить ориентироваться в потоке информации. Особо сложно работать с текстами на уроках математики, так как тексты учебника информационные, содержат много терминов, не всегда написаны понятным для школьника языком. Всё это затрудняет самостоятельную работу учащихся с текстом.

Поэтому у учителя математики возникают вопросы:  какие приёмы работы с тестом выбрать, где, при изучении какой темы ими можно будет воспользоваться, чтобы они были более эффективны.

Приведенные модели уроков  примерные. На конкретном уроке, с данными детьми, вопросы могут быть другими.

Образование должно быть рассчитано на перспективу, должно строиться на основе двух неразлучных принципов: умения быстро ориентироваться в стремительно растущем потоке информации и находить нужное, и умения осмыслить и применить полученную информацию.

Целевой компонент урока

Педагогические цели

1. Развивать мышление, математическую речь; учить работать с математическим текстом.
2. Организовать индивидуальную работу; работу в парах или группах по выполнению учебных заданий.

Ожидаемые результаты

1. Учащиеся вдумчиво читают текст, умеют выделять основные аспекты в изучаемой информации, формируют умение графически представлять результаты работы с текстом.
2. Учащиеся зримо демонстрируют процессы продвижения от незнания к знанию
3. Учащиеся анализируют, сопоставляют, логически мыслят, обобщают
4. Учащиеся умеют взаимодействовать в парах
5. Учащиеся, выступающие с защитой решений, демонстрируют владение математическим языком, знание текущего учебного материала
6. Учащиеся уважают одноклассников.

Используемые приёмы: кластеры, инсерт

Формы работы на уроке: коллективная, индивидуальная, работа в парах или в группах, в диалоге.

Оснащение урока: мультимедиа комплекс. Урок проводиться с использованием мультимедийной презентации PowerPoint.

План урока

Этапы урока	Деятельность учителя	Деятельность ученика	УУД
Вводно-мотивационный	Создание мотивации для работы на уроке Постановка цели урока Актуализация знаний по предыдущим темам	Приветствие Участие в беседе Выявление связей предыдущего материала и данного. Заполнение первичного кластера	Коммуникативные Коммуникативные Регулятивные, познавательные
Информационно-групповой	Организация парной, индивидуальной деятельности по вдумчивому прочтению текста учебника Учитель задаёт вопросы: По каким пунктам ваше мнение не изменилось, после прочтения текста? Что вы можете добавить в первоначальную схему?	Читают текст учебника, делают пометки карандашом на полях учебника « v» уже знал, «+» - новое, «?» - не понял. Ученики в тетрадях изображают свою схему. Ответы на поставленные вопросы	Познавательные, общеучебные, коммуникативные Общеучебные, коммуникативные Регулятивные
Рефлексивный	Подведение итогов	Учащиеся вносят изменения в схему. Записывают домашнее задание	Регулятивные

 

Сценарий урока

Вводно-мотивационный этап.

Учитель: Сегодня на уроке мы будем говорить о площади многоугольника. Урок построим по следующему плану:

• вспомним, что мы уже знаем о площади многоугольника, оформим наши знания графически
• по работам с текстом учебника, вдумчиво прочитаем текст
• вернёмся к нашим предположениям, обсудим  - правы ли мы были, дополним наши ветви
• подведём итоги урока

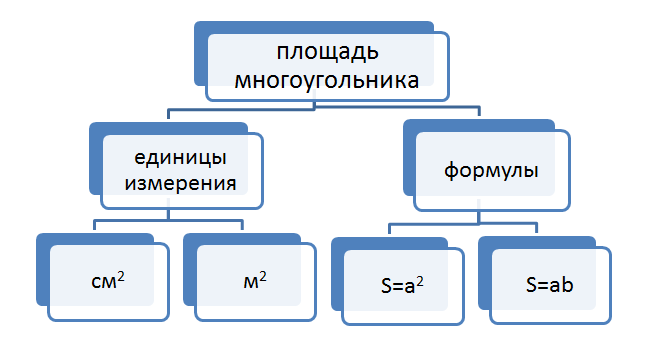
Учитель предлагает графически представить на доске всё, учащиеся знают по теме урока

Информационно-групповой этап

На этом этапе учащиеся читают текст учебника. Читая текст, стр. 117-122, учащиеся делают пометки на полях карандашом: « v» уже знал, «+» - новое,  «?» - не понял.

Учащиеся читают текст. После прочтения текста вновь возвращаются к графическому представлению. Посмотрим, может быть после прочтения текста, что то изменилось.

Учитель задаёт вопросы

• По каким пунктам ваше мнение не изменилось, после прочтения текста?
• Что вы можете добавить в первоначальную схему?

Ученики в тетрадях изображают свою схему.

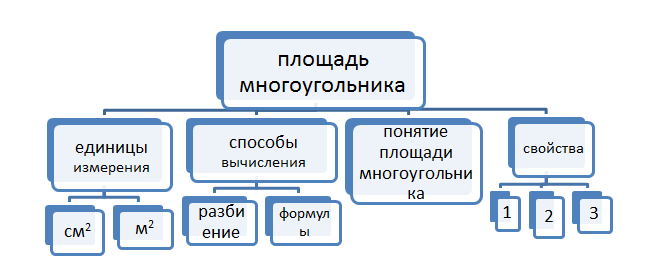
Рефлексивно-оценочный этап

Учитель: Подведём итоги.

Ученики на доске показывают свой вариант схемы. Сверяют её с  последним слайдом презентации.

Домашнее задание:

• подумать, чем ещё можно дополнить данную схему.

Уравнение cosx=a

Цель урока: научить понимать, как из таблицы часто встречающихся a получить значения арккосинуса а; познакомить с формулой для нахождения корней уравнение cosx=a, где 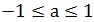  показать применение формул при решении несложных тригонометрических уравнений. Продолжить развитие навыков коммуникативной культуры.

Ход урока

В начале урока учитель предлагает записывать материал урока в виде таблицы. В левом столбце таблицы- слова учителя; в правом- предположения, возможные ответы учащихся.

Учитель	Учащиеся
Запишите формулы, по которым находятся решения уравнений cosx=0, cosx=1, cosx=-1
Что бы вы хотели узнать ещё по этой теме?	Как решаются уравнения cosx=a, где
Попытайтесь, работая в парах, придумать пути решения уравнения cosx=0,5,	cosx- абсцисса точки единичной окружности. Абсциссу равную 0,5 имеют две точки. Корни уравнения можно найти по формуле
Можно ли эти решения записать одной формулой?
Теперь попробуйте решить уравнение	х=?
Что бы дать ответ на поставленный вопрос, необходимы дополнительные знания. Где можно найти недостающею информацию?	В учебнике, в интернете

 

Далее учащимся предлагается поработать с учебником, стр. 224-226. На эту работу вам даётся 5 минут.

После окончания работы учитель предлагает учащимся поделиться своими мыслями с классом. Ответы записывают на доске. Далее учитель предлагает проверить записи сделанные учащимися в таблице.

После обсуждения остаётся  вопрос о решении уравнения .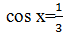

Создадим таблицу значений арккосинуса, для этого приведём таблицу значений косинуса

Из данной таблицы можно получить таблицу часто встречающихся значений арккосинуса

Теперь потренируемся вычислять, для этого выполним номера 719(1;3;5) 720(1;3;5) 721(1;3;5). Учащиеся записывают значения в тетрадь, обсуждают в группах, с классом обсуждаются вопросы, вызвавшие затруднения.

Учитель обращает внимание, что уравнение 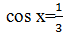 так и не решено, спрашивает у учащихся, хватит ли теперь знаний для решения этого уравнения.

Учащиеся записывают на доске решение этого уравнения, после пробуют решить .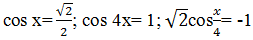

Учащиеся обсуждают ответы на каждое уравнение.

Учитель предлагает решить более сложное уравнение  cosxcos3x= sin3xsinx.

В ходе решения повторяется всё, что известно о решении уравнений, тригонометрические формулы, тождественные преобразования. Решение записывается на доске.

В заключении учитель предлагает учащимся составить алгоритм решения тригонометрического уравнения по материалу урока.

Список источников

1. Л. С. Атанасян, В. Ф. Бутусов, С.Б. Кадомцев и др. Геометрия, 7-9; Учеб. для общеобразоват.  учереждений /-М.: Просвещение, 2004
2. Л.В. Арьяева. Информационное взаимодействие в современной школе: опыт диалога. Монография. Санкт-Петербург 2012
3. С. И. Заир-Бек, И. В. Муштавинская. Развитие критического мышления на уроке: пособие для учителей общеобразоват.  учереждений-М.: Просвещение, 2011