Образовательный портал

Мастерская «Формы мышления. Алгебра высказываний»

Дорофеева Наталья Фёдоровна, Государственное бюджетное общеобразовательное учреждение Петергофская гимназия императора Александра II, учитель информатики.

Цель: создание условий для самореализации при решении логических задач.

Задачи:

- создать необходимые предпосылки для работы с научнопонятийным  текстом;

- научиться строить алгебраические высказывания, используя логические операции;

-уметь реализовать логические операции и строить таблицы истинности с помощью программы Excel.

Средства, пособия, материалы: карточки с определениями, какие бывают формы мышления и что такое «алгебра высказываний», карточки с примерами; карточки с пояснениями  к примерам и объяснением построения новых высказываний с помощью базовых логических операций; практические работы, подготовленные на листах, на построение таблиц истинности, которые реализуются в программе MSExcel.

Ход мастерской

Занятие 1.

Вступительное слово учителя. Здравствуйте, ребята! Тема нашего занятия: «Формы мышления. Алгебра высказываний». Она написана на доске.

Сегодня у нас урок-мастерская. Вы получаете задание, которое можете выполнять так, как его поняли. Неверно выполненных заданий не бывает, главное для нас попытаться его выполнить.  При выступлении слушаем не только себя, но и других. Попробуйте,  выполняя все задания - испытать  чувство радости успешно проделанной работы. Вы можете отказаться предъявить результаты работы или от выступления, но при этом надо слушать других.

Задания в мастерской выполняются сначала индивидуально, затем в группе.

1. Ребята, напишите фразу: ФОРМЫ МЫШЛЕНИЯ. Вслушайтесь, вдумайтесь в эти слова. Напишите звуковые, смысловые ассоциации; все, что приходит вам на ум, когда вы слышите фразу «формы мышления».

Давайте прочитаем, что у вас получилось.

1. Если в ваших ассоциациях встречаются термины: ПОНЯТИЕ, СУЖДЕНИЕ, УМОЗАКЛЮЧЕНИЕ, ВЫСКАЗЫВАНИЕ, УТВЕРЖДЕНИЕ – подчеркните их.
2. Из своих ассоциаций составьте предложение, «ФОРМЫ МЫШЛЕНИЯ – это……….».
3. Участники мастерской объединяются в пары.

Раздаю каждому ученику карточки с определением, что представляют собой ФОРМЫ МЫШЛЕНИЯ. Дополните своё определение или измените его. Обсудите в группе, придите к единому мнению по этому вопросу.

1. Вывешивание произведений учеников и мастера в аудитории и ознакомление с ними: все ходят, читают, обсуждают или зачитывает вслух автор, другой ученик, мастер.
2. Учащиеся остаются в парах. Мастер раздает карточки с примерами и пояснением к ним.  Ребята  обсуждают в группе, совпало ли их видение вопроса с истинным, высказываются по этому поводу.
3. Наше 1 занятие заканчивается. Хотелось бы услышать, комфортно ли вам работалось; что удалось, а может быть, не удалось, что мешало; с каким чувством вы уходите с мастерской.

Занятие 2.

Вступительное слово учителя.На первом занятии мы с вами давали объяснение, что же является формами мышления. На втором часе давайте познакомимся с другим новым для нас понятием АЛГЕБРА ВЫСКАЗЫВАНИЙ.

1. Попрошу вас на компьютере внимательно посмотреть видеоряд: Древняя Греция, страны Древнего Востока (Индия, Китай), обратите ваше внимание на мыслителей того времени  и их учения.

Вопросы ученикам: а) Скажите, пожалуйста, что объединяет эти картинки? (Участники мастерской высказываются по этому вопросу).

б) Запишите слова, которые у вас возникли при просмотре видеоряда.

2.  Добавьте к своим словам, слова – ЛОГИКА, АЛГЕБРА, ВЫСКАЗЫВАНИЕ, СОДЕРЖАНИЕ, УМОЗАКЛЮЧЕНИЕ, ПОНЯТИЕ, СУЖДЕНИЕ, УТВЕРЖДЕНИЕ.

Объедините два слова: АЛГЕБРА и ВЫСКАЗЫВАНИЕ во фразу « Алгебра высказываний», запишите её на листе посередине - это ваша тема текста.

1. Составьте небольшой текст, в который будет входить большинство терминов, о которых мы только что говорили.
2. Участники мастерской объединяются в пары.

Обсуждают в группе свои тексты, приходят к единому мнению.

Раздаю каждому лист с моей лекцией.  Прошу прочитать их внимательно.

5. Вывешивание произведений учеников и мастера в аудитории и ознакомление с ними: все ходят, читают, обсуждают или зачитывает вслух автор, другой ученик, мастер.

6. Прошу учащихся промаркировать мой текст, в следующем порядке: отметить знаком «+» - что они знают (им понравилось);

знаком «-» - не знаю;

знаком «?» - это хочу спросить.

С последнего маркера  мастер опрашивает ребят: «Какой вопрос вы хотите мне задать?», «Что осталось для вас непонятным?», «Что понравилось?», «Что было удивительным?».

7. Даю ребятам практические работы на составление таблиц истинности с помощью базовых логических операций, используя программную среду MSExcel.

Спасибо всем за прекрасную работу. Вы все хорошо потрудились, и мне очень приятно было вместе с вами учиться.

 Материалы к мастерской

Тексты на карточках.

А) Основными ФОРМАМИ МЫШЛЕНИЯ являются – ПОНЯТИЕ, СУЖДЕНИЕ и УМОЗАКЛЮЧЕНИЕ.

Б) ПОНЯТИЕ.

Выделяет существенные признаки объекта, которые отличают его от других объектов. Объекты, объединенные понятием, образуют некоторое множество. Пример: понятие «компьютер» объединяет множество электронных устройств, которые предназначены для обработки информации и обладает монитором и клавиатурой.

Понятие имеет 2 стороны: содержание и объем. Чтобы раскрыть содержание понятия, следует найти признаки, необходимые и достаточные для выделения данного объекта из множества других. Объем понятия определяется совокупностью предметов, на которые оно распространяется.

ВЫСКАЗЫВАНИЕ.

 Своё понимание окружающего мира человек формулирует в форме высказываний (суждений, утверждений). Высказывания могут быть выражены не только с помощью естественных языков, но и с помощью формальных языков.

Об объектах можно судить верно или неверно, т.е. высказывание может быть истинным или ложным. Истинным будет высказывание, в котором связь понятий правильно отражает свойства и отношения реальных вещей. Ложным высказывание будет в том случае, когда оно не соответствует реальной действительности.

На основании простых высказываний могут быть построены составные высказывания.

Пример: «Процессор является устройством обработки информации, и принтер является устройством печати» является составным, состоящим из двух простых.

Если истинность или ложность простых высказываний устанавливается в результате соглашения на основании здравого смысла; то истинность или ложность составных высказываний вычисляется с помощью использования алгебры высказываний.

УМОЗАКЛЮЧЕНИЕ.

Умозаключения позволяют на основе известных фактов, выраженных в форме суждений, получать заключение, т.е. новое знание. Пример: геометрические доказательства.

1. Лекция:

Алгебра высказываний была разработана для того, чтобы можно было определить истинность или ложность составных высказываний, не вникая в их содержание.

В алгебре высказываний суждениям (простым высказываниям) ставятся в соответствие логические переменные (заглавные буквы лат. алфавита).

Пример.Два высказывания:

• «2*2=4»;
• «2*2=5»

Истинному высказыванию соответствует значение логической переменной- 1, а ложному-0. В нашем случае 1-е (A=1), а второе (B=0).

В алгебре высказываний над высказываниями можно производить определенные логические операции, в результате которых получаются новые составные высказывания.

Для образования новых высказываний часто используют базовые логические операции, выражаемые словами «и», «или», «не».

Логическое умножение (конъюнкция).

Объединение двух (или нескольких) высказываний в одно с помощью союза «и».

Составное высказывание, образованное в результате операции логического умножения, истинно тогда и только тогда, когда истины входящие в него простые высказывания.

Операцию логического умножения принято обозначать: “^”, “&” или “*”.

Образуем составное высказывание F=A&B. Значение этой функции можно определить по таблице истинности:

 

 

A	B	F=A&B
0	0	0
0	1	0
1	0	0
1	1	1

 

Логическое сложение (дизъюнкция).

Объединение двух (или нескольких) высказываний в одно с помощью союза «или». Составное высказывание, образованное в результате операции логического сложения, истинно только тогда, когда истинно хотя бы одно из входящих в него простых высказываний.

Принято обозначать: либо «ˇ», либо «+».

F=AˇB. Значение этой функции можно определить по таблице истинности:

 

 

A	B	F=AˇB
0	0	0
0	1	1
1	0	1
1	1	1

 

Логическое отрицание (инверсия).

Присоединение частицы «не» к высказыванию. Логическое отрицание делает истинное высказывание ложным, и наоборот, ложное – истинным.

Принято обозначение Ā.

F= Ā. Значение этой функции можно определить по таблице истинности:

 

 

A	F= Ā.
0	1
1	0

 

Логическое следование (импликация).

Логическое следование образуется соединением двух высказываний в одно с помощью оборота речи «если….., то…..».

Обозначение: «Если Aто B» - A->B.

Составное высказывание, образованное с помощью операции логического следования ложно тогда и только тогда, когда из истинной предпосылки(первого высказывания) следует ложный вывод(второе высказывание).

 

 

A	B	F=A->B
0	0	1
0	1	1
1	0	0
1	1	1

 

1. Практические работы на составление таблиц истинности.

Карточка 1.

а) Из приведенных афоризмов Козьмы Пруткова высказываниями являются:

1. Смотри в корень!
2. Ветер есть дыхание природы.
3. Нет адъютанта без аксельбанта.
4. Почему сивый всегда завидует буланому?
5. Лучше скажи мало, но хорошо.
6. Усердие все превозмогает.

б)Составить таблицу истинности: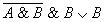

Карточка 2.

а) Из приведенных афоризмов Козьмы Пруткова высказываниями являются:

1. Новые сапоги всегда жмут.
2. Что есть хитрость?
3. Хитрость есть оружие слабого и ум слепого.
4. Не все стриги, что растет.
5. Никто не обнимет необъятного!
6. Всегда держись начеку!

б)Составить таблицу истинности: