Образовательный портал

Некоторые приемы работы над текстовыми задачами

Назаревская Светлана Дмитриевна,
учитель математики ГБОУ СОШ №188
с углубленным изучением Мировой
художественной культуры Санкт-Петербурга

«Не будет большим преувеличением утверждение о том, что жизненная деятельность человека и (общества) состоит из каждодневного решения различных задач во всем  разнообразии их содержания, роли и применяемых методов решения.  Большинство из этих, ставящихся жизнью задач, решается человеком (и обществом) в процессе целенаправленной и планомерной деятельности; некоторые из этих задач возникают случайно и требуют от человека принятия решения в незапланированном человеком порядке, вне зависимости от готовности и умения отдельного индивидуума решать их правильно. Решение многих задач требует от человека хорошо развитой способности к творческой деятельности». Эти слова принадлежат великому математику и педагогу Ю. М. Колягину.

Несомненно, эти слова остаются актуальны и в настоящее время.  Умение решать  задачи является одним из наиболее необходимых качеств интеллектуально-развитого человека.  Но к сожалению наши ученики не любят  задачи. Многие из них даже не приступают  к их решению.

На  уроках математики  я стараюсь научить своих учеников не только уметь решать задачи, но и не испытывать «страх перед ними».

Работа над обучением решать задачи ведется с первых уроков математики в 5 классе. Я учу своих учеников относится к любой задаче не как к еще одному заданию по математике, которое надо выполнить для отработки и сформированности тех или иных умений и навыков, а как к определенной житейской задаче, которая может возникнуть в той или иной ситуации.

Начинаю работу  над любой задачей с того, что:

1) Прошу учеников самостоятельно познакомиться с условием задачи.

2) Далее одного из учащихся прошу еще раз прочитать задачу вслух.  Ученик должен прочитать задачу так, чтобы условие задачи стало доступно каждому. Если учащийся читает условие задачи очень быстро или «проглатывает слова», то останавливаю его чтение и прошу его же или другого ученика прочитать условие медленнее и выразительнее.

2) После четкого, разборчивого и выразительного чтения задачи прошу учащихся рассказать о той ситуации, которая происходит в данной задаче.

В своем рассказе ученики не должны использовать цифры, которые присутствуют в условии задачи, т.к. цифры не дают полного представления о той или иной ситуации, и чаще всего отвлекают учащихся от восприятия тех событий, которые происходят в данной жизненной ситуации. (Иногда, невозможно пересказать условие задачи без данных цифр, но я прошу в своем рассказе как можно реже их использовать). Нужно уметь при решении любой задачи выделять главное, не обращать  внимание на второстепенные вещи.

3) Одним из важнейших этапов в работе над задачей я считаю умение записать условие задачи в виде  краткой записи.

Это может быть перечень объектов, о которых говорится в данной задаче,  чертеж, иллюстрирующий  условие  задачи, или таблица.

 

Задача № 1.Одна сторона четырехугольника равна 7 м, вторая – на 5 дм больше первой, а третья – в 3 раза меньше второй. Найдите четвертую сторону этого четырехугольника, его периметр равен 23 м. ( Г.В. Дорофеев, Л.Г. Петерсон  5 класс, часть 1)

Задача № 2. Андрей ехал на автомашине из станицы в город со скоростью 55 км/ч. На всю дорогу он потратил 2 часа. Из города в станицу он ехал по той же дороге, но на мопеде со скоростью 22 км/ч. За сколько времени Андрей доедет до станицы?  ( Н.Я. Виленкин, В.И. Жохов и др. Математика, 5 класс)

  

 Задача № 3. Из двух пунктов, расстояние между которыми 40 км, навстречу друг другу одновременно отправились пешеход и велосипедист. Скорость велосипедиста в 4 раза больше скорости пешехода. Найдите скорости пешехода и велосипедиста, если известно, что они встретились через 2,5 часа после своего выхода?  (Н.Я. Виленкин, В.И. Жохов и др. Математика, 6 класс)

     

Задача № 4.На четырех полках 180 книг. На первой полке в 2 раза больше книг, чем на второй, а число книг на третьей полке составляет 60% от числа книг на второй и 2/3 от числа книг на четвертой полке. Сколько книг на каждой полке? ( Г.В. Дорофеев, Л.Г. Петерсон  6 класс, часть 2)

 

 

 

Задача № 5.В первом мешке было 50 кг сахара, а во втором – 80 кг. Из второго мешка взяли сахара в 3 раза больше, чем из первого, и тогда в первом мешке сахара осталось вдвое больше, чем во втором. Сколько килограммов сахара взяли из каждого мешка?

 

	Было	Изменилось	Стало
I м.	50 кг	- ?  в 3 р. Б.	В 2 р. Б.
IIм.	80 кг	?

 

Задача № 6.Сме­ша­ли не­ко­то­рое ко­ли­че­ство 10-про­цент­но­го рас­тво­ра­ не­ко­то­ро­го ве­ще­ства с таким же ко­ли­че­ством 12-про­цент­но­го рас­тво­ра ­это­го же ве­ще­ства. Сколь­ко про­цен­тов со­став­ля­ет кон­цен­тра­ция по­лу­чив­ше­го­ся рас­тво­ра? ( Сдам ГИА, Д. Гущин)

 

	Раствор	проценты	вещество
Было	Х	10 %	0,1 х
Добавили	Х	12 %	0,12 х
Стало	Х+Х	?	0,1 х + 0,12 х

 

 

Задача № 7. Теп­ло­ход про­хо­дит по те­че­нию реки до пунк­та на­зна­че­ния 165 км и после сто­ян­ки воз­вра­ща­ет­ся в пункт от­прав­ле­ния. Най­ди­те ско­рость теп­ло­хо­да в не­по­движ­ной воде, если ско­рость те­че­ния равна 4 км/ч, сто­ян­ка длит­ся 5 часов, а в пункт от­прав­ле­ния теп­ло­ход воз­вра­ща­ет­ся через 18 часов после от­плы­тия из него. ( сдам ГИА, Д. Гущин)

	V км/ч	t ч	S км
По течению	? + 4 км/ч	tст = 5 ч	165 км
Против течения	? – 4 км/ч	tоб = 18 ч	165 км

 

 

Задача № 8.Одна из дорожных бригад может заасфальтировать некоторый участок дороги на 4 ч быстрее, чем другая. За сколько часов может заасфальтировать участок каждая бригада, если известно, за 24 ч совместной работы они заасфальтировали 5 таких участков? (Ю. Н. Макарычев, Н.Г. Миндюк и др. Алгебра, 9 класс)

                                            Отдельнаяработа:

	V	t дн.	A
Iбригада	1/ х-4	На 4 ч меньше	1
IIбригада	1/х	Х	1

                                                     Совместнаяработа.

Iбригада	1/ х-4
IIбригада	1/х	24 ч	5 уч.

 

Краткая  запись условия  задачи помогает учащимся отбросить лишнюю информацию  и сосредоточиться на главных данных задачи.

Я считаю, что в каждой таблице название и расположение столбиков должно логически подводить к выбору действий и связи между компонентами в задаче.

Так, например, физические формулы, которые помогают в решении задач, записываю с учащимися не так, как они выглядят в действительности, т.е. на уроках физики.

В начальной школе ученики в основном решают задачи по действиям. После записи действия учащиеся чаще всего записывают пояснение. Если в предложенной задаче необходимо найти стоимость предметов, то они знают, что надо цену одного предмета умножить на количество таких предметов; если в задаче надо найти  массу предметов, то ученики  вес одного предмета умножают на количество таких предметов; если же надо найти расстояние, то  учащиеся скорость умножают на время; и т.д.

Поэтому я считаю, что и в таблицах необходимо столбики называть так, чтобы у учащихся не возникало вопросов какое действие необходимо выбрать, чтобы найти ту или иную величину.

Каждый столбик таблицы связан с последующим определенным знаком:

«Цена» * «Количество» = «Стоимость».

«Урожай с одного га» * «Площадь участка» = «Общей массе».

«Скорость» * «Время»= «Расстояние».

«Производительность» * «Время» = «Работа».

Краткая запись помогает учащимся не только проанализировать задачу, но и облегчить само решение задачи.

4) Когда в курсе математики появляются задачи, которые решаются только при помощи уравнения или системы уравнений, то после оформления краткой записи я составляю и записываю «связующее» выражение.

Рассмотрим задачу № 5 (см. выше):  В первом мешке было 50 кг сахара, а во втором – 80 кг. Из второго мешка взяли сахара в 3 раза больше, чем из первого, и тогда в первом мешке сахара осталось вдвое больше, чем во втором. Сколько килограммов сахара взяли из каждого мешка?

 

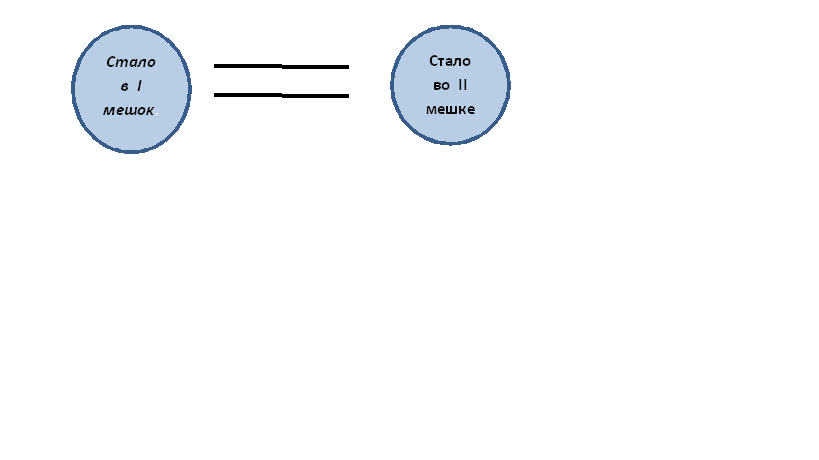
Далее я предлагаю учащимся представить весы.

«Пусть на одной чашечке весов находится сахар, который остался в первом мешке, а на второй чашечке весов сахар, который остался во втором мешке».

Затем задаю ученикам  вопрос: «Можно ли поставить знак равно между данными величинами?»

Учащиеся отвечают:

 «Между данными величинами знак равно поставить нельзя, т.к. в задаче говориться, что после того, как из обоих мешков взяли сахар, то в первом мешке сахара осталось больше».

«Как же можно уравнять чаши воображаемых весов?»

 

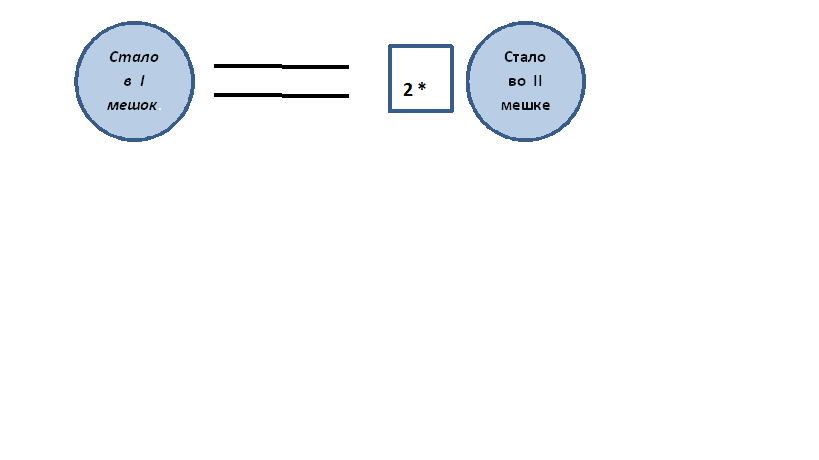
«Что нужно сделать, для того чтобы узнать, сколько стало сахара в каждом мешке?»

«Надо из сахара, который был в мешке вычесть тот, который взяли».

Мы продолжаем работать со «связующим» схемой.

 

 

 

По данной схеме любой ученик может составить уравнение.      

Интересно наблюдать за учениками, когда при самостоятельном решении задачи, они приподнимают перевернутые вверх ладошки , изображая предполагаемые весы,  и поднимая то одну ладошку, то другую, мысленно уравнивают чашечки своих весов.

Спустя некоторое время многие учащиеся на черновике делают «связующие» схемы и не используют краткую запись условия задачи в виде таблицы.   

  5) Следующий этап работы над задачей очень важен для учащихся, т.к. он способствует развитию их логического мышления.

После схематической записи условия задачи необходимо провести анализ условия и составить план решения.

В 5 – 6 классах в основном задачи решаются по действиям.

Анализ задачи чаще всего провожу от главного вопроса к условию задачи.

«Что надо узнать в данной задаче?»

«Можно ли сразу ответить на главный вопрос задачи?»

«Почему?» и т.д.

Задача.

В зоопарке было 35 львов, носорогов, обезьян и крокодилов. Львов было 6, носорогов на 2 меньше, чем львов, а обезьян в 5 раз больше, чем носорогов. Сколько крокодилов было в этом зоопарке? ( Г.В. Дорофеев, Л.Г. Петерсон, Математика, 5 класс)

1)      Краткая запись условия задачи:

 

2)      Анализ условия задачи:

 

Что надо узнать в этой задаче? ( Сколько в зоопарке крокодилов).

Можно ли сразу ответить на главный вопрос задачи? ( Нет).

Почему? ( Мы не знаем, сколько в зоопарке львов, носорогов и обезьян вместе).

Можно ли узнать сразу, сколько в зоопарке львов, носорогов и обезьян вместе?

( Нет).

Почему? ( Нам неизвестно, сколько в зоопарке носорогов и сколько обезьян).

Можно ли узнать, сколько в зоопарке носорогов? ( Да).

Какое условие задачи нам поможет найти количество носорогов в зоопарке?

( Носорогов в зоопарке на 2 меньше, чем львов).

Каким действием мы сможем узнать количество носорогов в зоопарке?

 ( Вычитанием).

Докажите, что количество носорогов в зоопарке вы сможете найти вычитанием.

( В условии задачи говорится, что носорогов на 2 меньше).

Можно ли узнать, сколько в зоопарке обезьян? ( Да).

Почему? ( Т.к. мы нашли количество носорогов и по условию задачи знаем, что обезьян в 5 раз больше, чем носорогов).

Каким действием вы узнаете количество обезьян? ( Умножением).

Докажите, что количество обезьян действительно можно узнать умножением.

( В условии задачи сказано, что обезьян в 5 раз больше).

Можно ли теперь узнать, сколько в зоопарке крокодилов? Если нет, то почему?

( Нельзя, т.к. мы не узнали, сколько в зоопарке львов, носорогов и обезьян вместе).

Можно ли теперь узнать, сколько в зоопарке этих зверей? ( Да).

Каким действием вы узнаете, сколько в зоопарке львов, носорогов и обезьян вместе? ( Сложением).

Можно ли теперь узнать, сколько в зоопарке крокодилов? ( Да).

Каким действием вы найдете количество крокодилов? ( Вычитанием)

 

3)      Проанализировав условие задачи, составляем план решения.

 

Ребята, составьте план решения задачи. Расскажите, что вы узнаете сначала, а что потом.

( Сначала мы найдем количество носорогов, потом – обезьян, следующим действием, сколько всего в зоопарке львов, носорогов и обезьян, а далее найдем количество крокодилов в этом зоопарке).

 

4)      Запись решения задачи.

После составленного плана учащиеся пробуют записать решение задачи в тетради.

Это тоже достаточно сложный процесс для некоторых учеников. Учителю во время оформления учащимися решения задачи лучше всего пройти по классу и может быть кому-то из своих учеников напомнить план решения задачи.

 

5)      Проверка записи решения задачи.

Через определенное время решение задачи высвечивается на экране интерактивной доски. Если нет экрана, то можно одного из учеников попросить параллельно с записью решения задачи классом вести запись на меловой доске, или решение задачи спрятать за шторкой на доске.

Данный анализ и разбор решения задачи поможет в дальнейшем на уроках геометрии работать с геометрическими задачами и приучает учащихся выстраивать логическую цепочку решения задачи.

6) Если задача имеет несколько решений, то после записи решения обязательно задаю вопрос классу: «Можно ли данную задачу решить другим способом?»

Этот этап работы над задачей тоже нельзя недооценивать, т.к. другой способ решения является:

1)      проверкой решенной задачи;

2)       возможностью найти более рациональное решение;

3)      возможностью некоторым учащимся проявить свою инициативу и не следовать конкретному (порой навязанному учителем) способу решения.

Автор статьи поделилась некоторыми приемами работы над задачами, которые помогают ее учащимся успешно решать многие задачи, предлагаемые для решения в школьном курсе математики и алгебры.

Не надо забывать, что, к сожалению, в современных учебниках математики мало места уделяется нестандартным задачам, в основном в учебных пособиях предлагаются «шаблонные» задачи. Но и «шаблонные» задачи по мнению известного венгерского, швейцарского, американского  математика  Д. Пойа «могут быть полезными или даже необходимыми,  если они даны в правильное время и  правильной дозе».

Известный советский математик Софья Александровна Яновская (1896-1966), выступая перед участниками математических олимпиад, неожиданно для слушателей на вопрос «Что значит решить задачу?», ответила, что «Решить задачу – значит свести ее к уже решенным».

Поэтому решение «шаблонных» задач способствует и решению нестандартных задач.

Решение математических задач очень важный процесс школьного обучения учащихся, т.к. способствует развитию не только развитию интеллектуальных способностей учеников, но и развитию таких качеств, как находчивость, сообразительность, смекалка, терпение, настойчивость, воля и стремление добиться успеха, преодолевая трудности.

Работа над задачами на уроках математики отвечает всем требованиям новых стандартов ФГОС, т.к. сам процесс решения задач и правильно организованная методика способствуют развитию у учащихся:

 «алгоритмического мышления, необходимого для профессиональной деятельности в современном обществе»;

 « умений составить и записать алгоритм для конкретного исполнителя»;

 формированию:

 « знаний об алгоритмических конструкциях, логических значениях и операциях» (Приказ Министерства образования и науки Российской федерации от 6 октября 2009г № 413 ОБ УТВЕРЖДЕНИИ И ВВЕДЕНИИ В ДЕЙСТВИЕ ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО ОБРАЗОВАТЕЛЬНОГО СТАНДАРТА).

Литература:

1.      Приказ Министерства образования и науки Российской федерации от 6 октября 2009г № 413 ОБ УТВЕРЖДЕНИИ И ВВЕДЕНИИ В ДЕЙСТВИЕ ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО ОБРАЗОВАТЕЛЬНОГО СТАНДАРТА;

2.      Приказ Министерства образования и науки Российской федерации от 17 декабря 2010 г. № 1897 «ОБ УТВЕРЖДЕНИИ ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО ОБРАЗОВАТЕЛЬНОГО СТАНДАРТА ОСНОВНОГО ОБЩЕГО ОБРАЗОВАНИЯ»;

3.      Пойа Д. Как решать задачу. - Львов: Квантор, 1991;

4.      Колягин Ю.М., Оганесян В.А. Учись решать задачи/ Ю.М. Колягин, В.А. Оганесян – М: Просвещение, 1982

5.      Методика преподавания математики в средней школе: Общая методика: Учеб. Пособие для студентов пед. Ин-тов по спец. 2014 «Математика» и 21056 «Физика» / А.Я. Блох, Е.С. Канин и др.; сост. Р.С. Черкасов, А.А. Столяр. – М. 1985

6.      Фридман Л.М., Турецкий Е. Н. Как научиться решать задачи/ Л.М. Фридман, Е.Н. Турецкий – М.: Просвещение, 1989

7.      Колягин Ю.М., Оганесян В.А. Методика преподавания математики в средней школе. Общая методика.  Учеб. пособие для студентов физ.-мат.фак. пед.институтов. М., Просвещение, 1975

8.      С. А. Гастева, Б. И. Крельштейн, С.Е. Ляпин, М. М. Шишловская, Методика преподавания математики в восьмилетней школе. Пол общей ред. С.С. Ляпина, М. : Просвещение, 1965