Образовательный портал

Учебно-методическое пособие
"Логические основы построения компьютера"

Чеботарева Евгения Александровна,
учитель информатики ГБОУ СОШ № 35 
Василеостровского района Санкт-Петербурга

Методическая разработка представлена в виде набора текстовых учебно-методических материалов по теме "Логические основы построения компьютера" Эти материалы могут использоваться как учителем для проведения урока, так и учеником для самостоятельного изучения данной темы на уроке в школе или дистанционно дома.
Каждый урок содержит презентацию по теории, набор заданий для самостоятельной работы ученика и домашнее задание. Так же в web-сайт включены справочные материалы, задания для контрольной работы и свободно распространяемая игра "Логический тренажер". 
Данную работа выполнена в рамках такого метода обучения как Кейс-технологии.

·           Кейс- технологии - технологии, основанные на комплектовании наборов (кейсов) текстовых учебно-методических материалов и рассылке их обучающимся для самостоятельного изучения.

Кейс-технология позволяет установить оптимальное сочетание теоретического обучения и практических навыков. Для этого необходимо чтобы кейс отвечал поставленной цели при его создании и использовании, имел несколько уровней трудности, развивал аналитическое мышление, содержал примеры практического применения изучаемого материала. Кейсы могут быть различной направленности и использоваться на разных этапах изучения темы или дисциплины в целом, различают:
- Кейсы, иллюстрирующие проблему или концепцию в целом. Этот тип чаще всего используют для начала изучения больших тем, таких как "Пакет MS Office". 
- Кейсы, обучающие практическим навыкам и умениям. Данный тип кейсов основывается на применении уже полученных теоретических знаний и позволяет отработать практические навыки по заданной теме. 
-Кейсы, обучающие решению проблем и принятию решений. 
-Кейсы, обучающие анализу и оценке своих действий. 
Работа с кейсом может быть задана на любой стадии урока 

По программе  курса информатики и ИКТ Макаровой Н.В. данная тема изучается в 9 классе в разделе "Техническое обеспечение информационных технологий". 

На изучение темы отводится 8 часов занятий в классе и 5 часов на самостоятельную работу учащихся. 

Урок 1 - Основные понятия алгебры логики.

Урок 2-3 - Логические выражения и операции.

Урок 4 - Составление таблиц истинности по логической формуле.

Урок 5 - Определение логического выражения по таблице истинности.

Урок 6-7 - Логические элементы и основные логические устройства компьютера.

Урок 8 - Контрольная работа

Содержание обучения соответствует углубленному базовому уровню.

Содержание обучения:

Основные понятия алгебры логики. Понятие высказывания. Логические выражения и логические операцииЖ НЕ, ИЛИ, И, ЕСЛИ..., ТО.., эквивалентность. Таблицы истинности.

Составление таблиц истинности по логической формуле. Законы булевой алгебры. Определение логического выражения по таблице истинности.

Логические элементы и основные логические устройства компьютера.

 

Учащиеся должны знать:

·           что такое высказывание;

·           таблицы истинности основных логических операций: НЕ, ИЛИ, И, ЕСЛИ..., ТО..., эквивалентность;

·           правила построения таблиц истинности основных логических выражений;

·           правило определения логического выражения по таблице истинности;

·           что такое логические элементы компьютера и как они используются при проектировании схем.

Учащиеся должны уметь:

·           написать таблицу истинности для основных логических операций;

·           построить таблицу истинности для логического выражения;

·           записать логическое выражение на основе таблицы истинности.

Тематическое планирование учебного материала

 

№	Тема	количество часов		§
		теория	практика
1	Основные понятия алгебры логики	1		23.1
2	Логические выражения и логические операции	1	1	23.2
3	Составление таблиц истинности по логической формуле		1	23.3
4	Законы булевой алгебры. Упрощение логических выражений.	0,5	0,5	23.4
5	Определение логического выражения по таблице истинности.		1	23.5
6	Логические элементы и основные логические устройства компьютера.	1	1	23.6
7	Контрольная работа	1
Итого:		4,5	4,5

Урок № 1

Основные понятия алгебры логики

• Теория

Алгебра логики — это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними.

Алгеброй логики называется аппарат, который позволяет выполнять действия над высказываниями.

Алгебра логики возникла в середине ХIХ века в трудах английского математика Джорджа Буля.

Высказывание - это предложение, относительно которого имеет смысл говорить истинно оно или ложно.

Примеры:    

Москва - столица России	истинное высказывание
На улице идет снег	предложение не является высказыванием, так как не указан город, время и т. д.
Информация - это сведения об объектах окружающего мира	предложение не является высказыванием, так как это определение
2+2*5=12	истинное высказывание
Закрой, пожалуйста, окно	предложение не является высказыванием, так как нельзя сказать истинно оно или ложно
Все ученики - отличники	ложное высказывание
2*x+6=0	предложение не является высказыванием, так как не указано, для какого x определяется истинность высказывания

Чтобы обращаться к логическим высказываниям, им назначают имена - прописные латинские буквы.

Алгебра логики рассматривает высказывания не с точки зрения  их содержания, а с точки зрения их истинности или ложности. Можно сказать, что высказывание может принимать только два значения - ИСТИНА ( обозначается 1) и ЛОЖЬ ( обозначается 0)

• Задания для самостоятельной работы

Задание № 1

Определите являются ли предложения высказываниями и какими - истинными или ложными. 

а) Солнце - спутник Земли;

б) 2+3/4;

в) сегодня отличная погода;

г) в романе Л.Н. Толстого "Война и мир" 3 432 536 слов;

д) Санкт-Петербург расположен на Неве;

 

Задание № 2

Приведите примеры истинных и ложных высказываний :

а) из арифметики;

б) из физики;

в)из биологии;

Задание № 3

Прочтите текст и определите истинны или ложны следующие высказывания:

Тест в Excel

	истина	ложь
Джордж Буль - известный английский математик.
Джордж Буль - преподавал в начальной школе математику.
Именем Джорджа Буля назван раздел геометрии.
В 1848 году Джордж Буль опубликовал статью по началам математической логики.
Основными операциями булевой алгебры являются конъюнкция (И), импликация (ЕСЛИ-ТО), равнозначность (А тогда и только тогда, когда В).

 

Джордж Буль

George Boole

(02.11.1815 – 08.12.1864)

Джордж Буль родился в Линкольне (Англия) в семье мелкого торговца. Материальное положение его родителей было тяжелым, поэтому Джордж смог окончить только начальную школу для детей бедняков; в других учебных заведениях он не учился. Этим отчасти и объясняется, что , не связанный традицией, он пошел в науке собственным путем. Буль самостоятельно изучил латынь, древнегреческий, немецкий и французский языки, изучил философские трактаты. С ранних лет Буль искал работу, оставляющую возможности для самообразования. После многих неудачных попыток Булю удалось открыть маленькую начальную школу, в которой он преподавал сам. Школьные учебники по математике привели его в ужас своей нестрогостью и нелогичностью, Буль вынужден был обратиться к сочинениям классиков науки и самостоятельно проштудировать обширные труды Лапласа и Лагранжа.
В связи с этим занятием у него появились первые самостоятельные идеи. Результаты своих исследований Буль сообщил в письмах профессорам математики (Д.Грегори и А.де Моргану) знаменитого Кембриджского университета и вскоре получил известность как оригинально мыслящий математик. В 1849 году в г.Корк (Ирландия) открылось новое высшее учебное заведение – Куинз колледж, по рекомендации коллег-математиков Буль получил здесь профессуру, которую сохранил до своей смерти в 1864 году. Только здесь он получил возможность не только обеспечить родителей, но и спокойно, без мыслей о хлебе насущном, заниматься наукой. Здесь же он женился на дочери профессора греческого языка Мери Эверест, которая помогала Булю в работе и оставила после его смерти интересные воспоминания о своем муже; она стала матерью четырех дочерей Буля, одна из которых, Этель Лилиан Буль, в замужестве Войнич, - автор популярного романа "Овод".

Джордж Буль по праву считается отцом математической логики. Его именем назван раздел математической логики - булевая алгебра. В 1848 году Джордж Буль опубликовал статью по началам математической логики - "Математический анализ логики, или Опыт исчисления дедуктивных умозаключений", а в 1854 году появился главный его труд "Исследование законов мышления, на которых основаны математические теории логики и вероятностей". В этих работах отразилось убеждение Буля о возможности изучения свойств математических операций, осуществляемых не обязательно над числами. Ученый говорил о символическом методе, который он применял как к изучению дифференцирования и интегрирования, так и к логическому выводу и к теоретико-вероятностным рассуждениям. Именно он построил один из разделов формальной логики в виде некоторой "алгебры", аналогичной алгебре чисел, но не сводящейся к ней.

Буль изобрел своеобразную алгебру - систему обозначений и правил, применимую ко всевозможным объектам, от чисел до предложений. Пользуясь этой системой, он мог закодировать высказывания (утверждения, истинность или ложность которых требовалось доказать) с помощью символов своего языка, а затем манипулировать ими, подобно тому как в математике манипулируют числами. Основными операциями булевой алгебры являются конъюнкция (И), дизъюнкция (ИЛИ), отрицание (НЕ).
Через некоторое время стало понятно, что система Буля хорошо подходит для описания электрических переключателей схем. Ток в цепи может либо протекать, либо отсутствовать, подобно тому как утверждение может быть либо истинным, либо ложным. А еще несколько десятилетий спустя, уже в ХХ столетии, ученые объединили созданный Джорджем Булем математический аппарат с двоичной системой счисления, заложив тем самым основы для разработки цифрового электронного компьютера.

Газета "ИНФОРМАТИКА «Аристотель, Лейбниц, Буль»

• Домашнее задание

1. Какие из предложений являются высказываниями? Определите их истинность.

а) Все ученики - мальчики.

б) Кто пойдет в кино?

в) Посмотрите в окно.

г) Все люди смелые.

д) Некоторые собаки не любят кошек.

2. Приведите примеры истинных и ложных высказываний из истории развития вычислительной техники.

Урок №2-3

Логические выражения и операции

• Презентация по теории

Урок 2-3

• Задания для самостоятельной работы

Задание № 1

Подставьте  в  приведённые  ниже  высказывательные  формы  вместо логических переменных а, Ь, с, А такие высказывания, чтобы полученные таким образом составные высказывания имели смысл в повседневной жизни: 
    а) если (а или (b и с)), то с;

Задание №2
Пусть а = "это утро ясное", а b — "это утро теплое". Выразите следующие формулы на обычном языке:

 

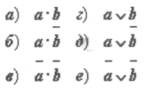
Задание № 3 

Для какого символьного выражения верно высказывание: ¬ (первая буква согласная) & ¬ (вторая буква гласная)?

1)аЬсdе     2) bcadе     3)babas     4) саbab

Задание № 4

Ниже в табличной форме представлен фрагмент базы данных:

№	Страна	Столица	Площадь, тыс. км2	Численность населения, млн. чел.
1	Бельгия	Брюссель	30,5	10289
2	Бурунди	Бужумбура	27,8	6096
3	Гаити	Порт-о-Пренс	27,8	7528
4	Дания	Копенгаген	43,1	5384
5	Джибути	Джибути	22,0	0,457
6	ДоминиканскаяРеспублика	Санто-Доминго	48,7	8716
7	Израиль	Тель-Авив	20,8	6116
8	Коста-Рика	Сан-Хосе	51,1	3896
9	Лесото	Масеру	30,4	1 862

Сколько записей в данном фрагменте удовлетворяют условию:

(Плошадь тыс. км²) > 20) И (Численность населения, млн. чел.) > 1 500))И(Часть света = Африка)

Задание № 5

В таблице приведены запросы к поисковому серверу. Расположите обозначения запросов в порядке убывания количества страниц, которые найдет сервер по каждому запросу. Для обозначения логической операции ИЛИ в запросе используют знак | , для логической операции И - &.

a	спорт|футбол
b	спорт| футбол| Петербург| Зенит
c	спорт| футбол| Петербург
d	спорт& футбол& Петербург& Зенит

• Домашнее задание

1. Подставьте  в  приведённые  ниже  высказывательные  формы  вместо логических
переменных а, Ь, с, ё такие высказывания, чтобы полученные таким образом составные
высказывания имели смысл в повседневной жизни:

б) если (не а и не b),то (с или d);

2. Пусть а = "это утро ясное", а b = "это утро теплое". Выразите следующие формулы на обычном языке:

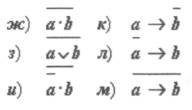
Урок № 4

Составление таблиц истинности по логической формуле

• презентация по теория

Урок 4

• Задания для самостоятельной работы

Задание № 1

Постройте таблицы истинности для логических формул

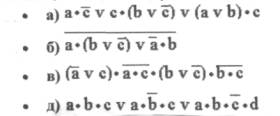
Задание № 2

Запишите в виде логической формулы следующие высказывания, обозначив:

А - Турист поехал в Турцию, 

В - Турист поехал в Грецию. 

• Турист поехал или в Грецию, или в Турцию. 
• Турист не поехал ни в Грецию, ни в Турцию. 
• Если турист поехал в Грецию, то он не поехал в Турцию.

Задание № 3

Какое логическое выражение эквивалентно выражению НЕ(А И В)->C?

1)НЕ А И В И С

2) АVВVС

3)НЕ (А и В) и С

4)НЕ А и НЕ В и НЕ С

Задание № 4

Районный отдел трудоустройства осуществляет начальное обучение (1 группа) или повышение квалификации (2 группа) людей, которые по каким-либо причинам ищут работу. Особое внимание уделяется слушателям, входящим "в группу риска". Это люди, которым "за 40", и они или не имеют в настоящее время работы, или пришли в группу начального обучения. Какая логическая формула отражает отбор в группу риска?

1. И(Возраст>40) ИЛИ(Работа="-";Группа=1).

2. ИЛИ(Возраст>40;Работа=" -" ;Группа=1). 

3. И(Возраст>40; ИЛИ(Работа="-";Группа=1)). 

4. И(Возраст>40;Работа="-" ;Группа=1).

Задание № 5

В таблице истинности указаны значения трех логических переменных: А, В и С. Запишите в столбце значения, соответствующие логическому выражению F = А Ù В ÙØ С.

А	В	С	F
0	0	0
0	0	1
0	1	1
1	0	0
1	0	1
1	1	0
1	1	1

Домашняя работа

Задание №1 

Запишите в виде логической формулы следующие высказывания, обозначив: А -Число делится на 3, В - Число делится на 9. 

а) Число делится и на 3, и на 9. 

б) Число не делится ни на 3, ни на 9. 

в) Если число делится на 9, то оно делится и на 3.

Задание № 2

Постройте таблицы истинности для логических формул

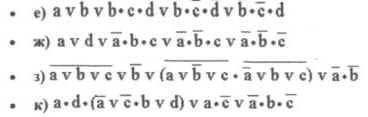
Задание № 3

В классе оказалось разбито стекло. Учитель объясняет директору:" Это сделал Саша или Коля. Но Саша этого не делал, так как в это время сдавал мне зачет. Следовательно это сделал Коля. Прав ли учитель? 

 

Урок № 5

Законы булевой алгебры

Определение логического выражения по таблице истинности

• презентация по теории

Урок 5

• Задания для самостоятельной работы

Задание № 1

Имеются две логические переменные: А и В. Упростите логическое выражение F, составленное из этих переменных: F = (А  И  В) V (НЕ А  И  В) V (А  И  НЕ В) V (НЕ А  И  НЕ  В)Определите, как зависит упрощенное выражение F от значений А и В?

Задание № 2

Имеются две логические переменные: А и В. Упростите логическое выражение F, составленное из этих переменных:

F = (А  И  В) V (НЕ А V НЕ В)

Задание № 3

Дана таблица истинности: 

X	Y	?
0	0	1
0	1	1
1	0	0
1	1	0

Какому логическому выражению она соответствует? 

Задание № 4

Имеются три логические переменные: А, В и С. Напишите логическое выражение соответствующее следующей таблице истинности, и упростите его.

A	B	C	F
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	0
1	0	0	0
1	0	1	0
1	1	0	1
1	1	1	1

Задание № 5

Какое из выражений эквивалентно логической формуле
(А V В) & (А V (НЕ В))?

1. А&В

2. А

3. А V В.

4.  В & (А V В).

• Домашнее задание

1. Имеются три логические переменные: А, В и С, из которых составлено логическое выражение:

F = (А  И  В И  НЕ  С) V (НЕ А  И  В И  НЕ С) V (В  И  С).

Упростите логическое выражение F и определите, значения каких переменных влияют на значение F.

2. Студентам, получающим стипендию и принимающим участие в жизни вуза (хотя бы в одном из проводимых мероприятий: конференция, олимпиада, конкурс), деканат добавляет к стипендии 10%. Какая логическая формула отражает условие получения надбавки? 

1. И(Стипендия; ИЛИ(Конференция; Олимпиада; Конкурс)). 

2. ИЛИ(Стипендия; Конференция; Олимпиада; Конкурс). 

3. И(Стипендия; Конференция; Олимпиада; Конкурс). 

4. И(Стипендия); ИЛИ(Конференция; Олимпиада; Конкурс).

3. Имеются две логические переменные: А и В. Составьте и упростите логическое выражение F соответствующее следующей таблице истинности

A	B	F
0	0	1
0	1	1
1	0	0
1	1	0

Уроки № 6-7

Логические элементы и основные логические устройства компьютера

• презентация по теории

Урок 6-7

• Задания для самостоятельной работы

Задание № 1

На оба входа приведенной логической схемы подается один и тот же сигнал А, который может принимать значения "1" (истина) или "0" (ложь).

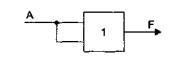
Какое значение будет на выходе F схемы?

Задание № 2

Дана логическая схема. 

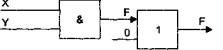
При каких значениях X и Y на входе схемы на ее выходе F будет "1" (истина)?

Задание № 3

На один вход логической схемы И подается сигнал А, который может принимать значения "1" (истина) или "0" (ложь), на другой - его отрицание.

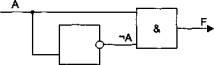
 Какое значение будет на выходе схемы?

Задание № 4

Запишите формулу, отражающую логическое преобразование, выполняемое схемой.

Задание № 5

Запишите логическую функцию, описывающую состояние данной логической схемы, и составьте таблицу истинности.

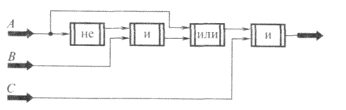
Задание № 6

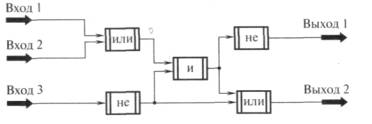
Составьте таблицу истинности по следующей схеме:

 

• Домашнее задание

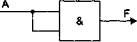
1. На оба входа приведенной логической схемы подается один и тот же сигнал А, который может принимать значения "1" (истина) или "0" (ложь). Какой закон Булевой алгебры иллюстрирует схема?

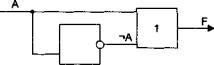
2. На один вход логической схемы ИЛИ подается сигнал А, который может принимать значения "1" (истина) или "0" (ложь), на другой - его отрицание . Какое значение будет на выходе схемы?

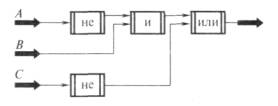
 3. Запишите логическую функцию, описывающую состояние данной логической схемы, и составьте таблицу истинности.

Урок № 8 Контрольная работа.

 

Литература

1.     Н.В. Макарова "Программа по информатике и ИКТ" 5-11 класс, Питер, СПб, 2007

2.     "Информатика и ИКТ  учебник 8-9 класс" под редакцией Н.В. Макаровой, Питер, СПб, 2007

3.     Л.З. Шауцукова "Информатика 10-11" - http://book.kbsu.ru

4.     O.В. Суворов "Основы логики" , "Аквариум", М., 1997

5.     В. Курбатов "Как развить свое логическое мышление", "Зевс", М., 1997

6.     Л.А. Анеликова "Раздаточные материалы по информатике 7-9 классы" часть I, Дрофа, М., 2004

7.     Макарова Н.В. Подготовка к ЕГЭ. Питер, СПб, 2007

8.     Семакин И.Г., Хеннер Е.К, Информатика. Задачник - практикум. Москва,2000

9.     О.В.Суворов.Основы логики для средней школы.М.,Аквариум,1997.

Презентации  к урокам и текст контрольной работы размещены на http://pr-sch35.ucoz.ru в разделе Методические материалы.